Contents
ランダム・ウォーカーとは
こんにちは。
金融教育研究所の佐々木裕平です。
ちょっとサイコロを振ってみましょう。
サイコロを振ると、各目の出る確率は、完全に独立していることが分かります。
どういうことでしょうか。
サイコロの出る目は過去と関係性がない
たとえば、1の目が連続9回出たとします。
次に1の目が出るかどうかは、結局1/6の確率です。
まあ、当たり前ですね。
サイコロには意思がなく、あくまでもランダム(独立・でたらめ)に出るわけですから。
つまり、サイコロの出る目は独立しています。
独立しているということは、ランダムなのです。
ですから、仮にサイコロの出る目を過去にさかのぼって、チャート分析をしても、法則性がない、わけです。
独立に動く、ランダム・ウォーカーには、チャート分析・テクニカル分析が通用しないことになります。
サイコロの出る目は、それぞれ1/6の確率。
次にサイコロを数千万回振ってみましょう。
すると、各目の出る確率は、おそらく限りなく1/6に近づいていくと期待できます。
数回程度では、ランダムなのですが、6面体ですから、確率上は、振る回数を増やすと、1/6に近づいていくのですね。
これも当り前のお話です。
ちなみにこれを「大数の法則」といいます。
かっこいいですね(笑)。
サイコロを6回振ると、出る目の平均は3.5になると期待できる
では今度は、サイコロを6回振ってみましょう。
その6回振った目の合計÷6は、いくらになるでしょうか。
つまり、6回振ると、平均値はいくらになるか、ということです。
6回振るのを1セットとします。
数回程度では、結果がばらつきます。
- 1連続して6回出て、平均が1になることもあります
- 6連続で6が出て、平均が6になることもあります
では、数千万セットサイコロを6回振ると、その平均値はどうなると期待されるでしょうか?
1+2+3+4+5+6=21
21÷6=3.5になります。
ですから、計算上は、数万セットサイコロを6回振ると、その平均値は3.5になると期待されます。
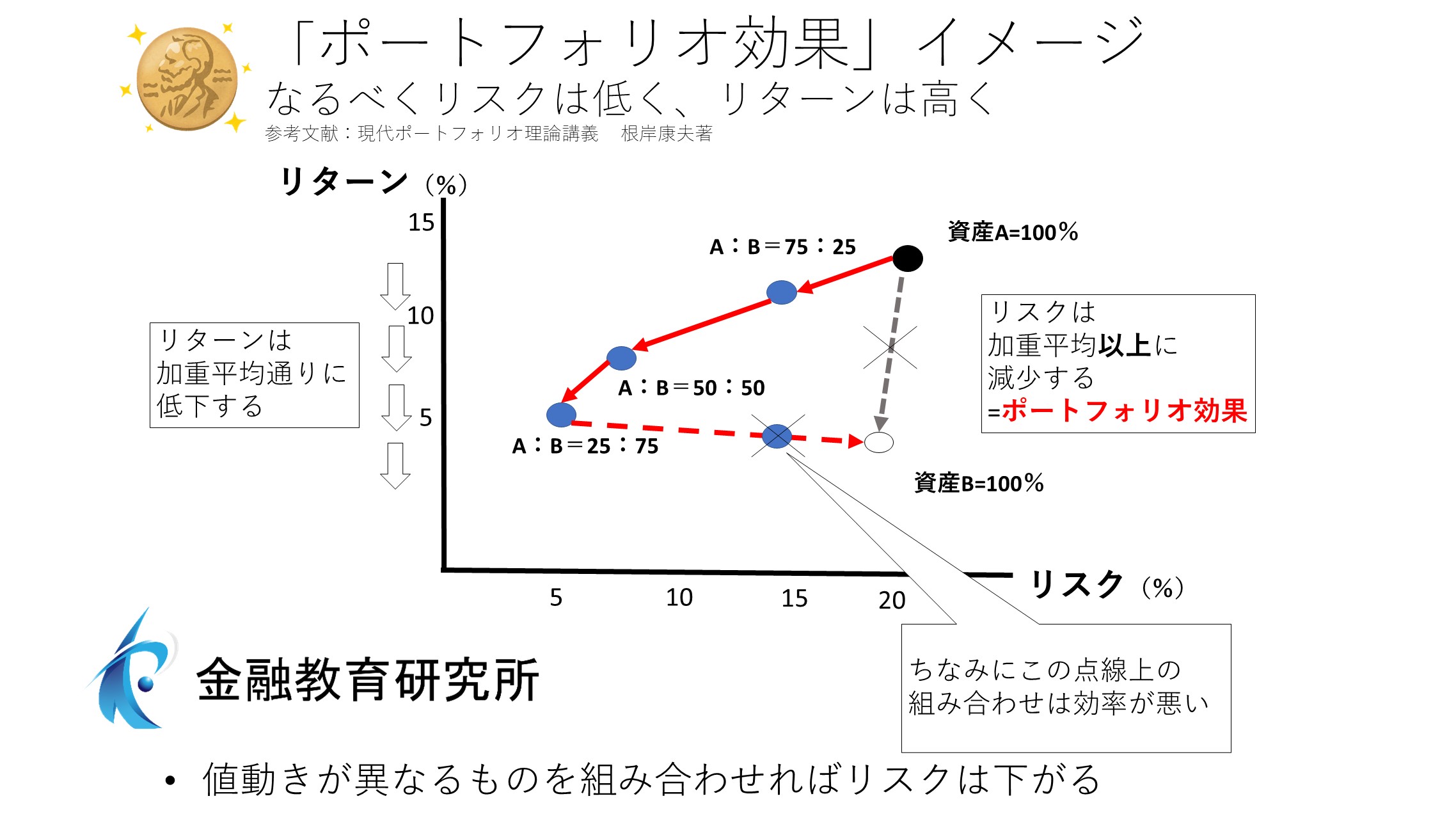
株式投資の場合、分散していると、この3.5にあたる数字(年率5~6%程度)が期待リターン=市場・投資家の要求リターンになるということです。
つまり、この場合のサイコロの期待リターンにあたるのは3.5になるということです。
サイコロの触れる幅は、1~6の間に正規分布する
では今度は、6回サイコロを振った場合の平均値は、どのくらいの振れ幅になるでしょうか。
この振れ幅のことを、標準偏差=リスクと、資産形成では言います。
先ほど見たように、一番可能性が少ないもので、
- 1連続して6回出て、平均が1になることもあります
- 6連続で6が出て、平均が6になることもあります
となります。
ですから、数万セット、6回サイコロを振る行為を行うと、
1~6までの平均値に触れます。
この振れ幅=標準偏差=リスクです。
独立して、ランダムなものの平均値は、正規分布する
でも、期待される平均値は、1/6ずつではありません。
一番多く期待される平均値は、3.5でした。
さっきみた数字ですね。
そして一番少ないのは1と6です。
つまり、釣り鐘状のグラフになります。
3.5が一番高い確率密度で、1と6が左右にもっとも小さくなる、という釣り鐘型です。
この釣り鐘型になることを、統計学では正規分布する、という風に言います。
カッコいいですね(笑)。
投資の世界では、独立して動く株式は、ランダム・ウォーカーになる
ではここで株式投資を見てみましょう。
株式市場の株価の値動きは独立しています。
過去と相関性がない、サイコロの出る目と同じなのです。
これは市場が効率的な場合にそうなります。
そのため、独立している株価はランダム・ウォーカーになります。
サイコロと同じです。
つまり、チャート分析が通用しない。
ランダム・ウォーカーで動く、独立して法則性のない株式は、釣り鐘型になり、リスクと期待リターンが分かる
でも、だからこそ独立している株価の値動きに分かることがあります。
値動きを観測すると、釣り鐘型になるということです。
そこから、値動きの振れ幅=標準偏差=リスクが分かります。
そして、一番高い期待される平均値もわかります。
つまり、株式の期待リターンがわかる、ということです。
株式投資をするなら、短期のランダム・ウォーカーではなく、長期の期待リターンに期待する方が良いのではないか
ここから見えること。
それは、資産形成をするなら、でたらめな結果になる短期投資ではなく、
釣り鐘状の期待リターンに期待する、長期投資が合理的なのではないか、ということです。
非常に面白いですね。
それではまた。












_001-250x250.jpg)
_001-1-250x250.jpg)