Contents
平均回帰性 極端に触れても、平均に戻ってくる性質がある
こんにちは。
金融教育研究所の佐々木裕平です。
統計学は専門ではありませんが、資産形成のリスク(標準偏差)を考えていると、どうしても統計の知識が必要になってきます。
そもそも、リスク(標準偏差)とは、統計学的にリターンの確率密度を表したものです。
また、リターンの散らばり(リスク=標準偏差)は、平均回帰性がある、と考えられます。
この平均回帰性とは、どのような物でしょうか。
これは例えばバッターの打率のようなものです。
平均打率三割のバッターがいるとします。
十打席連続で三振したとします。
でも、この場合、次の十打席では、平均打率に近い成果が出るでしょう。
また反対に、十打席連続でホームランを放ったとします。
でも、次の十打席では、平均打率に近い成果が出るでしょう。
リターン(結果)は散らばり(リスク=標準偏差)があるのですが、
極端にどちらかに触れると、平均値に戻ってきやすい、という性質があるのですね。
統計で良く出る? さいころで例えてみましょう。
六面体のサイコロを六回振ります。
その目の合計の平均値はいくらでしょうか?
1+2+3+4+5+6=21 21÷6=3.5 です。
つまり、サイコロを6回振った場合の平均値は確率密度が最も高いのは、3.5なのです。
とはいえ、あくまでも確率密度が3.5が高いだけです。
毎回必ず3.5になるわけではありません。
もしかしたら、2セット連続で、平均が1になるかもしれません。
1+1+1+1+1+1=6 6÷6=1
つまり、12回連続で1ばかり出る、可能性があるのですね。
しかし、当然ながら、その可能性は低い。
三セット目、四セット目と、繰り返すほどに、平均値の3.5に近い数値が出てきます。
これは6であっても同様です。
これが平均回帰性である、と私は認識しています。とはいえ、統計学の専門家ではありませんので、違っておりましたら、ご容赦ください。
つまり、良い・悪い結果にたまたま偏ったとしても、長期で見ると、やがて平均値に戻ってくる、来やすいということです。
これを資産形成・投資の運用で考えると、どうなるでしょうか。

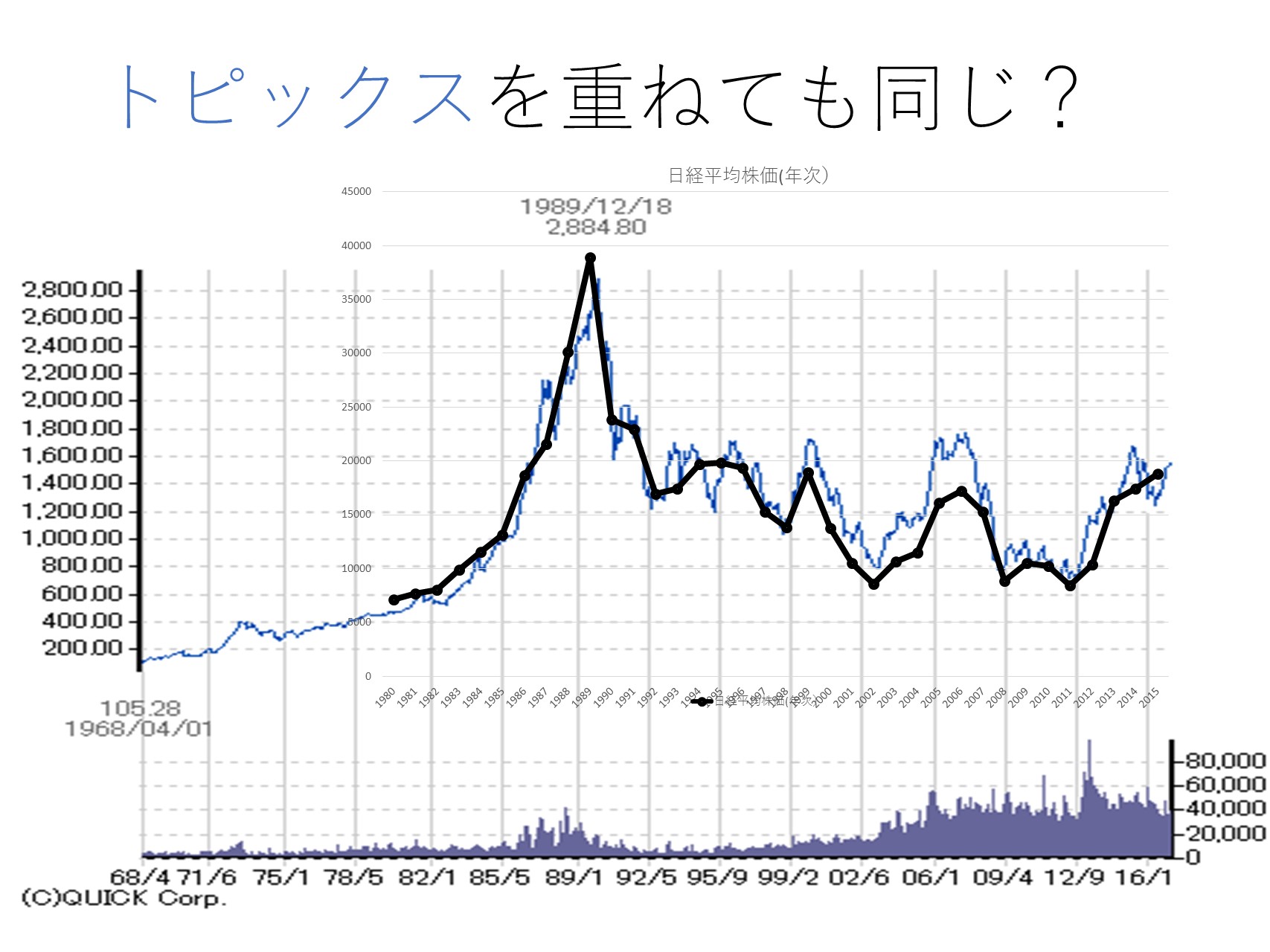
株価などはランダム・ウォーカーです。
これは、サイコロの出目のように、法則性がなく、ランダム(でたらめ)に動きます。
過去と関係なく、独立して動きます。
しかし、サイコロと同じように、完全にランダムな値動きをするもの(ランダム・ウォーカー)であると、
サイコロの平均値3.5のように、リターンのバラつき(リスク=標準偏差)は正規分布することになります。
ここが重要なことですが、ランダム・ウォーカーなものは、皮肉? なことに、正規分布するのです。
ですから、平均値=期待リターンとなります。
期待リターン=(市場が効率的ならば)投資家・市場の要求リターンです。
しかし、期待リターンが平均値とは言え、サイコロの3.5のように、3.5ばかりが出るわけではありません。
極端に悪い(バブル崩壊・コロナショック)年や、極端に良い(バブル期・危機脱却後)年が存在します。
そしてその極端な年は、ずっと続かない可能性があります。
なぜか? 平均回帰性があるからです。
極端に良い・悪い結果の年であっても、いえ、あるほどに、やがて平均値(期待リターン)に近い数値に戻っていきます。
では運用の場合、重要なことは何なのか?
それは、株価などはランダム・ウォーカーではあるが、平均回帰性がある、ということを理解しておくこと、ではないでしょうか。
それではまた。
いつでも、どこでも、だれでも、無料で、動画で学べる【お金の学校】のお知らせ
金融教育研究所の【お金の学校】をYouTubeにて継続的にアップしています。
ブログ記事よりも、よりわかりやすく、学びやすくなっています。
よろしければ、ご覧ください。
また、チャンネル登録や「いいね」をしていただきますと、とてもうれしいです!
どうぞよろしくお願いいたします。






-01-A納品用①-2-830x510.jpg)






_001-250x250.jpg)
_001-1-250x250.jpg)